Quindi è tutto così affascinante... la teoria delle stringhe è veramente una rivoluzione per la fisica! Dice che le particelle elementari non sono punti indivisibili, ma minuscole stringhe unidimensionali lunghe circa 10^-35 metri (sulla scala di Planck che definisce i limiti estremi dell'universo in termini di spazio, tempo ed energia). Sono quindi queste stringhe che vibrando in modi diversi producono gli elettroni, i quark, i fotoni e i gravitoni (la particella della gravità quantistica).
Così come le note di una chitarra nascono dalle vibrazioni di una corda, abbiamo che la massa, la carica e lo spin derivano dalle "armonie" di queste stringhe fondamentali.
Per coerenza matematica, la teoria richiede 10 o 11 dimensioni totali: le 4 che tutti noi conosciamo (3 spaziali + il tempo) più altre 6 o 7 "arrotolate" su varietà di Calabi-Yau microscopiche, che purtroppo sono invisibili a tutti gli attuali esperimenti.

Questa meravigliosa struttura unifica la relatività generale di Einstein con la meccanica quantistica, e di fatto risolve il conflitto della gravità quantistica che è essenziale per modellare i buchi neri e il Big Bang. Le implicazioni cosmologiche sono profonde: le stringhe modellano quella che viene chiamata "inflazione cosmica post-Big Bang" attraverso l'uso di "semplici" campi scalari che evitano così le singolarità iniziali della teoria, mentre le stringhe cosmiche giganti e le D-brane (le membrane multidimensionali) spiegano la struttura a grande scala dell'universo.

L'aspetto più importante e rivoluzionario è il cosidetto "paesaggio delle stringhe": con 10⁵⁰⁰ modi possibili di compattare le dimensioni extra ovvero i modi per ridurre le dimensioni spaziali aggiuntive che sono previste dalla matematica della teoria ad una scala così piccola da risultare invisibili all'osservazione diretta.
Ogni configurazione genera un diverso "vuoto" con costanti fisiche proprie: masse di particelle, forze e costante cosmologica, e questo produce un "multiverso eterno" di "universi bolla".
In questo multiverso eterno la nostra realtà è solo una bolla stabile in un mare infinito di possibilità. Leonard Susskind e altri fisici propongono quello che chiamano il principio antropico: osserviamo cioè un universo regolato perfettamente per la vita (tecnicamente con espansione accelerata dall'energia oscura) poiché è solo in queste bolle che emergono degli osservatori come lo siamo noi (le altre bolle collassano subito o si espandono troppo velocemente con il risultato di essere senza stelle e quindi senza galassie).

Il multiverso risolve il problema che viene chiamato "fine-tuning cosmologico" con la conseguenza che tutte le costanti sono perfette e funzionano perfettamente, perfette perché il nostro "mondo" è la scelta statistica perfettamente funzionante in tutto, tra un numero elevatissimo di mondi sterili o imperfetti. Così l'inflazione eterna generando continuamente nuove bolle, rende il nostro universo anche parte di un processo dinamico, e le onde gravitazionali generate dalle collisioni tra le brane o "big rip" ci rivelano i multiversi vicini a noi.

L'importanza è chiaramente epocale: la teoria delle stringhe promette una "teoria del tutto", ridefinendo il cosmo come un "ensemble" multidimensionale. Ispira ricerche su materia/energia oscura (supersimmetrica) come LIGO in USA e Virgo a Pisa che con i loro enormi interferometri laser che rilevano gli echi gravitazionali, o come i telescopi come Euclid (ESA) per la materia oscura e JWST (NASA/ESA/CSA) per l'infrarosso.

Se questa teoria verrà verificata svelerà l'origine ultima della realtà, trasformando definitivamente la scienza, la filosofia e la cosmologia come la conosciamo adesso, ed aprendo la strada a tecnologie future ad oggi fantascientifiche come la manipolazione dimensionale.

Un giovane fisico teorico salì sulla montagna per incontrare il maestro Zen.
Portava con sé quaderni pieni di equazioni, diagrammi e ipotesi.
Maestro - disse - studio la teoria delle stringhe. Mi dicono che tutto ciò che esiste è una vibrazione fondamentale. Ma io non riesco a capire che cosa sia davvero una stringa.
Il maestro non rispose subito. Prese una corda sottile, la tese tra due pioli e la pizzicò con calma. La corda produsse un suono profondo, regolare.
Questa - disse il maestro - è una particella.
Il fisico osservò attentamente - Maestro, quello che vedo è un’onda. Un moto periodico. Nella mia lingua direi: un modo normale di vibrazione.
Il maestro annuì. - Nella tua lingua è corretto.
Poi pizzicò di nuovo la corda, questa volta con maggiore tensione. Il suono cambiò, diventando più acuto.
Ora - disse - questa è un’altra particella.
Il fisico rifletté: - Dunque la corda è la stessa, ma ciò che cambia è la frequenza. Come in musica: una sola corda può produrre molte note.
Il maestro sorrise: - Esattamente. La natura non costruisce molti strumenti: ne accorda pochi.
Il fisico si animò: - Allora massa, carica e spin sono come il timbro di un suono?
Il maestro non rispose. Avvolse lentamente la corda attorno a un piccolo cilindro, lasciandola vibrare ancora. Il suono si fece più complesso, quasi impercettibile.
Quando lo spazio è semplice - disse il maestro - la musica è semplice. Quando lo spazio si avvolge su se stesso, la musica diventa ricca.
Il fisico riconobbe l’allusione alle dimensioni extra, alle strutture compatte che determinano i modi consentiti di vibrazione.
Maestro - chiese - possiamo ascoltare queste note? Possiamo misurarle?
Il maestro smorzò la corda con un dito. Il suono cessò. - Quando ascolti con strumenti grossolani - disse - le note più sottili non si sentono.
Il fisico tacque.
Dopo un lungo silenzio domandò: - Allora l’universo è musica?
Il maestro rispose: - No. La musica è solo un modo umano di riconoscere le vibrazioni.
Il fisico rifletté ancora. - E la teoria delle stringhe? È una descrizione vera dell’universo?
Il maestro sorrise, posò la corda e disse: - È una partitura. Non è l’esecuzione. Ma senza partitura, l’orchestra non suonerebbe.
Il giovane fisico si inchinò. Capì che non stava cercando una risposta, ma un’armonia.

L’universo è una grande orchestra e ogni particella è una nota, ogni forza una melodia, e l’intero cosmo una sinfonia di vibrazioni.
La Teoria delle stringhe ci dice che tutto ciò che esiste — elettroni, quark, luce e gravità — potrebbe essere il risultato delle diverse vibrazioni di minuscole corde di energia.
Ma come si passa dalle particelle alle corde? Secondo la fisica classica e quantistica, la materia è composta da particelle puntiformi e la teoria delle stringhe le sostituisce con corde unidimensionali: ciò che percepiamo come una particella è, in realtà, una stringa che vibra con una certa modalità.
Così, come in una chitarra, la frequenza di vibrazione determina il tipo di particella: una nota dà origine a un elettrone, un’altra a un quark, e così via...
Per fare in modo che queste stringhe possano vibrare in modo coerente, la matematica richiede alcune dimensioni extra dello spazio-tempo.
Queste dimensioni non sono visibili, ma “arrotolate” su se stesse in forme complesse chiamate Varietà di Calabi-Yau.
Proprio come le cavità di uno strumento musicale determinano il suono che produce, le dimensioni extra influenzano il modo in cui le stringhe vibrano, e quindi le leggi della fisica che normalmente sperimentiamo.
Nella fisica delle particelle, i processi di interazione vengono spesso rappresentati con i Diagrammi di Feynman.
Anche nella teoria delle stringhe si possono utilizzare rappresentazioni grafiche similari, ma in queste rappresentazioni i punti d’incontro non sono più vertici ma superfici che si deformano, si uniscono o si separano, proprio come le corde di uno strumento che entrano in risonanza.
La teoria delle stringhe è elegantissima, ma purtroppo ancora senza prove sperimentali. Le energie necessarie per “vedere” una stringa sono enormi, ben oltre le capacità degli acceleratori di particelle odierni. Tuttavia, il suo fascino resta intatto: è la prima teoria che unifica la gravità con le altre forze fondamentali, e che offre una visione coerente dell’universo in molte dimensioni.

“Se le stringhe vibrano, allora l’universo suona. E noi siamo le sue note.”

Un diagramma di Feynman è un grafo che rappresenta in modo schematico come interagiscono le particelle elementari secondo la meccanica quantistica e le teorie di Gauge (teoria QED e teoria QCD).

Questi diagrammi non descrivono esattamente quello che avviene nello spazio-tempo reale, ma è "semplicemente" un metodo per evitare di utilizzare integrali complessi.

Il diagramma di Feynman è uno strumento molto utile perché graficamente mostra quali particelle sono coinvolte in un processo e quali interazioni fondamentali stanno agendo (interazione elettromagnetica, forte o debole).

Per utilizzarle si deve definire l'asse che identifica lo scorrere del tempo (orizzontale, verticale).


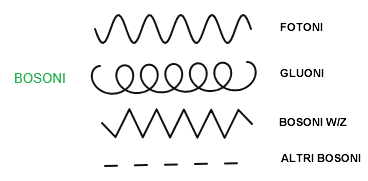
E si utilizzano i simboli che rappresentano le particelle e le interazioni.
In particolare le linee rette con una freccia rappresentano i Fermioni (le particelle di materia), ovvero i quark, gli elettroni, i neutroni, .. . Se la freccia ha lo stesso verso del tempo è una particella, se invece il verso è opposto è una anti-particella.


Le linee ondulate rappresentano l'energia (le particelle mediatrici) ovvero fotoni, gluoni, bosoni W/Z. I Bosoni scambiati (fotoni, gluoni, ecc.) sono quasi sempre virtuali, cioè non esistono come particelle libere ma solo come intermedi dell’interazione.


Tutti i vertici sono i punti in cui le particelle interagiscono e si scambiano i bosoni. I vertici rappresentano le interazioni dove sono rispettate le leggi di conservazione (dell'energia, del momento, della carica, ecc.).


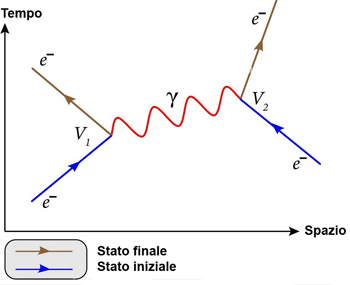
Ogni retta e ogni vertice ha una corrispondente equazione matematica e la disposizione delle rette, ovviamente, non rappresenta la posizione reale delle particelle nello spazio ma serve solo a conoscere quali sono le particelle che entrano nel processo e quali sono quelle escono.

Eugenio Calabi nacque a Milano l'11 marzo 1923 e morì a Bryn Mawr in Pennsylvania il 25 settembre 2023 all'età di 100 anni.
La sua famiglia era ebrea e, a causa delle leggi antisemite del governo italiano, fu costretta a emigrare nel 1939 negli Stati Uniti. All'età di 16 anni Calabi si iscrisse al MIT Massachusetts Institute of Technology, dove studiò ingegneria chimica. Nel 1943 si arruolò nell'esercito americano e solo alla fine della Seconda Guerra Mondiale riuscì a completare i suoi studi.

Nel 1947 conseguì un master in matematica presso l'Università dell'Illinois a Urbana-Champaign e successivamente nel 1950 conseguì il dottorato presso l'Università di Princeton con la tesi intitolata "Isometric complex analitic imbedding of Kähler manifolds" supervisionata da Salomon Bochner.

Dopo aver insegnato in diverse università, Calabi entrò nel 1964 a far parte della facoltà di matematica dell'Università della Pennsylvania dove trascorse il resto della sua carriera professionale.

Calabi diede contributi chiave in molti ambiti della geometria, perseguendo sempre la sua visione di affrontare problemi su cui nessuno aveva mai lavorato prima.
Il suo lavoro più influente è indiscutibilmente quello diventato noto come "La congettura di Calabi".
La congettura di Calabi, avanzata nel 1953, era relativa a una classe di varietà che ammettono anche coordinate complesse (la varietà è uno spazio localmente simile a uno spazio euclideo e può quindi essere dotato di coordinate locali che variano in modo diverso). Queste varietà sono chiamate varietà Kähleriane e potrebbero avere nulla la cosiddetta "curvatura di Ricci".

Nell'ambiente accademico la sua dimostrazione non fu unanime e per tale motivo un altro dei grandi matematici del secolo scorso, Shing-Tung Yau (allora di stanza a Berkeley) nel 1970 iniziò a lavorarci cercando di trovare controesempi che la confutassero. Questi controesempi non erano però tali, come Yau si rese conto mentre rivedeva le argomentazioni su richiesta diretta di Calabi. Dopo molto lavoro Yau dimostrò invece l'esistenza di tali varietà, che divennero note come varietà di Calabi-Yau, un risultato che gli valse nel 1982 la Medaglia Fields.

Dopo questi risultati i fisici teorici proposero la teoria delle stringhe in uno spazio a dieci dimensioni, assumendo che le sei dimensioni aggiuntive allo spazio-tempo fossero compattificate, formando, appunto, una varietà di Calabi-Yau.

Eugenio Calabi vedendo che la sua scoperta era stata applicata alla fisica teorica ne rimase molto sorpreso dato che il suo intendimento era sempre stato solo nello studio della geometria differenziale.

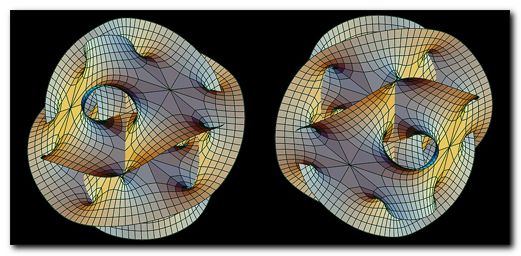
Immaginiamo il nostro universo come una torta a più strati. In questa torta-universo noi vediamo solo gli strati superiori che potrebbero essere le tre dimensioni dello spazio "più il tempo". Ma ecco che la fisica delle particelle ci dice che, in realtà, sotto la glassa della torta ci sono altre dimensioni che sono arrotolate su sé stesse e sono così piccole che non riusciamo a vederle.

Bene: se siamo riusciti a immaginarci questo possiamo dire che una varietà di Calabi–Yau è come la forma precisa dello “stampo” nella quale queste dimensioni extra sono arrotolate.

La varietà di Calabi–Yau ha delle proprietà matematiche molto eleganti: è “liscia” (nessun spigolo strano), e ha una specie di equilibrio interno perfetto assolutamente Zen.
Ovvero il volume interno è zero ma senza essere vuota, un po’ come un origami che occupa poco spazio ma è molto complesso.

Questa forma speciale permette alle stringhe, nella teoria delle stringhe, di vibrare nel modo "giusto" per generare tutte le particelle che conosciamo (e sicuramente anche quelle che non conosciamo ancora).

Ed ecco una connessione con la musica: se l’universo è un’orchestra, le stringhe sono gli strumenti e la varietà di Calabi–Yau è la sala da concerto nascosta che determina come risuona la musica.

Nella teoria delle stringhe, l’introduzione di dimensioni extra è necessaria per motivi matematici e fisici, legati alla coerenza interna della teoria e alla possibilità di unificare le forze fondamentali della natura.

Per evitare incoerenze matematiche, ovvero anomalie quantistiche, nella formulazione della teoria, le stringhe non possono vibrare in uno spazio di 3+1 dimensioni (cioè 3 spaziali + 1 temporale) senza generare contraddizioni.

Sono pertanto state formulate le stringhe bosoniche che richiedono 26 dimensioni per essere matematicamente consistenti e le superstringhe (più realistiche, includono anche fermioni e supersimmetria) che invece richiedono 10 dimensioni (9 spaziali + 1 temporale).

E' importante sottolineare che queste dimensioni aggiuntive non sono opzionali ma sono imposte dalla matematica altrimenti la teoria non funziona.

Abbiamo anche che le particelle elementari (elettroni, quark, fotoni, ...) sono viste come diverse modalità di vibrazione di una stringa e le diverse vibrazioni di una stringa richiedono gradi di libertà aggiuntivi per descriverle, cioè più direzioni in cui la stringa può oscillare. Pertanto più dimensioni.

Una delle ambizioni della teoria delle stringhe è unificare la gravità con le altre tre forze fondamentali (elettromagnetica, nucleare forte, nucleare debole) e questa unificazione richiede una struttura più ricca di quella offerta dal nostro spazio-tempo di "sole" 4 dimensioni.

Le dimensioni extra forniscono lo “spazio matematico” per far convivere, ad esempio, gravitoni (che mediano la gravità) e gluoni (che mediano l’interazione forte) all’interno della stessa teoria.

Per rispondere invece alla domanda di dove si possono trovare queste dimensioni extra, abbiamo che secondo la teoria, le dimensioni extra sono "compattificate", ovvero arrotolate su se stesse in spazi molto piccoli (es. spazi di Calabi-Yau), così piccoli da non essere percepibili direttamente.

Nell'estate del 1968, mentre era ospite del CERN, il fisico teorico Gabriele Veneziano scrisse un articolo intitolato "Construction of a crossing-symmetric, Regge behaved amplitude for linearly-rising trajectories". Con questo articolo cercava di spiegare l'interazione forte, invece l'articolo finì per segnare l'inizio della teoria delle stringhe.

Gabriele Veneziano in una intervista al CERN nel 2018 spiegò che:

"La reazione della comunità dei fisici fu per me uno shock... Non appena consegnai l'articolo, andai in vacanza e non ci pensai molto. Alla fine dell'agosto del 1968, partecipai a una conferenza a Vienna e scoprii, con mia sorpresa, che l'articolo era già ampiamente noto e menzionato in diverse presentazioni di sintesi".

L'articolo ebbe un successo immediato, afferma Veneziano, perché il modello rispondeva a diverse domande contemporaneamente. Ma in quel momento non era ancora evidente che avesse qualcosa a che fare con le stringhe, per non parlare della gravità quantistica, e poi nel 1973 altri fisici teorici dimostrarono questo collegamento cruciale.


"A quel punto divenne chiaro che il modello originale aveva una chiara interpretazione fisica degli adroni come stringhe quantizzate. Alcuni dettagli erano ovviamente sbagliati: una delle caratteristiche più sorprendenti delle interazioni forti è la loro natura a corto raggio, mentre uno stato privo di massa produce interazioni a lungo raggio. L'incoerenza del modello per tre dimensioni spaziali (il nostro mondo!) era anche imbarazzante, ma la gente continuava a sperare."

Nel decennio successivo, continua Veneziano, la maggior parte delle persone si tenne lontana dalla teoria delle stringhe. Il Modello Standard della fisica delle particelle era appena nato e c'era ancora molto da fare per estrarne le previsioni e testarlo.

"Ma cinquant'anni dopo, l'entusiasmo dei giovani teorici è ancora evidente e il campo è atipicamente giovane e forse ciò che motiva questi scienziati è la bellezza matematica della teoria delle stringhe, o la possibilità di eseguire molti calcoli diversi, pubblicarli e ottenere numerose citazioni."

Una domanda: Ma la teoria delle stringhe è vicina a descrivere la realtà?

“Si dice che la teoria delle stringhe non faccia previsioni, ma questo non è affatto vero. Prevede la dimensionalità dello spazio, ed è l'unica teoria finora a farlo, e predice anche, a livello di approssimazione più basso per una teoria relativistica quantistica, un'infinità di scalari privi di massa che minacciano il principio di equivalenza (l'universalità della caduta libera), ormai ampiamente testato. Se potessimo fidarci di questa previsione, la teoria delle stringhe sarebbe già falsificata. Ma lo stesso varrebbe per la cromodinamica quantistica (QCD), poiché implica l'esistenza di quark liberi e la tesi comune è che servano energie inconcepibilmente elevate per testare la teoria delle stringhe”.


La nuova incarnazione della teoria delle stringhe può essere falsificata da esperimenti a grande distanza, a patto che possiamo fidarci del livello di approssimazione con cui viene risolta. D'altra parte, per testare la teoria delle stringhe a breve distanza, il modo migliore è attraverso la cosmologia. Intorno (ovvero durante, prima o subito dopo) il Big Bang, la teoria delle stringhe potrebbe aver lasciato la sua impronta sull'universo primordiale e la sua successiva espansione può portarla oggi a scale macroscopiche.

La teoria delle stringhe è stata postulata per la prima volta nel 1968 dal fisico italiano Gabriele Veneziano che la introdusse nel mondo delle fisica due anni dopo.
La teoria venne creata per lo studio delle interazioni forti prima della formulazione della cromodinamica quantistica. La prima forma della teoria si chiamava teoria della stringa bosonica perché prendeva in esame solo i bosoni. Solo successivamente la teoria descrisse anche i fermioni (teoria delle superstringhe).
Prima del 1990 vennero pubblicate 5 teorie riguardanti le stringhe, ma successivamente si scoprì che erano tutti casi particolari di una sola teoria a 11 dimensioni che venne chiamata teoria M.

La teoria delle stringhe per ora non può essere dimostrata empiricamente dagli scienziati a causa del numero di dimensioni previste, anche perché la mente umana può concepirne solo tre (già nella teoria della relatività generale a quattro dimensioni ci sono alcuni problemi).
Anche se la teoria delle stringhe non è verificabile concretamente, alcuni studiosi della Towson University hanno ipotizzato che questa teoria si potrebbe dimostrare osservando il moto dei pianeti del sistema solare. Gli studiosi della Towson University sono convinti di poter trovare nuovi limiti alla teoria misurando le orbite planetarie aspettandosi la violazione del principio di equivalenza newtoniano.

La moderna teoria delle stringhe prevede che l'universo abbia undici dimensioni.
Le prime tre dimensioni sono le canoniche dimensioni spaziali che tutti conosciamo: la lunghezza, la larghezza e l'altezza.
Le altre otto dimensioni sono nascoste, ovvero non sono direttamente osservabili.
Le dimensioni nascoste sono anche molto piccole, nell'ordine di "10 alla -33" cm.
Sono così piccole che non si possono osservare con gli strumenti attuali.
Tuttavia, gli scienziati credono che queste dimensioni siano reali e che siano fondamentali nell'universo.

La teoria delle stringhe è una delle idee più ambiziose della fisica teorica moderna, ma ancora priva di conferme sperimentali.
Se questa teoria fosse corretta potrebbe spiegare in modo elegante l’intero universo, unificando così tutte le forze fondamentali dell’universo (gravità, elettromagnetismo, forza nucleare forte e debole).

La fisica teorica moderna cerca di unificare la relatività generale (che descrive la gravità su larga scala) e la meccanica quantistica (che descrive le interazioni fondamentali su scala microscopica).

La teoria delle stringhe invece di considerare le particelle elementari (come gli elettroni e i quark) come punti privi di dimensioni, propone che queste siano in realtà minuscole corde unidimensionali (chiamate "stringhe") che vibrano a diverse frequenze.

Queste vibrazioni determinano il tipo di particella osservato: un certo tipo di vibrazione corrisponde a un fotone (la particella della luce), un'altra vibrazione corrisponde a un quark (il componente fondamentale dei protoni e neutroni), e così via per tutte le particelle conosciute.

La teoria richiede più dimensioni spaziali oltre alle 3 che percepiamo. Le versioni più comuni parlano di 10 o 11 dimensioni, di cui 6-7 sarebbero "arrotolate" su scale infinitesimali (compattificazione di Calabi-Yau). La versione più accettata è la teoria delle superstringhe, che include la supersimmetria (ogni particella ha un cosiddetto partner super-simmetrico).
In alcune versioni, oltre alle stringhe, esistono oggetti chiamati "brane" (di diverse dimensioni) che potrebbero rappresentare l’universo stesso.

Una particolare vibrazione della stringa darebbe origine al gravitone, la particella ipotetica responsabile della gravità quantistica. Questo è uno dei motivi per cui la teoria delle stringhe è considerata una candidata per la "teoria del tutto".

Ma ad oggi ci sono ancora alcuni problemi: La teoria non è ancora verificabile sperimentalmente, le stringhe sono troppo piccole per essere osservate direttamente, la teoria prevede un numero enorme di universi possibili (multiverso) e purtroppo manca ancora una formulazione definitiva dato che esistono diverse versioni della teoria, ma non una teoria unificata.